Transformers - Fundamental Concepts with Python Implementation
Table of Contents
- Motivation - Why Transformers?
- Terminology
- Attention Mechanism: Learn by Example
- Transformer Models
- Coding a Simple Transformer
- Final Comments
1. Motivation - Why Transformers?
If you are interested in modern natural language processing (NLP), machine learning, and artificial intelligence, you probably need to learn Transformers and know how they can be implemented for various tasks. Transformers have set new benchmarks in a variety of NLP tasks such as language translation, text summarization, and question answering. Models like BERT, GPT-3, GPT-4, T5, LLaMA, and Claude are all implementing Transformers in their architectures. Transformers have also been adapted for use in other domains such as computer vision (Vision Transformers ViTs) and speech processing. One major advantage of Transformers, when compared with Recurrent Neural Networks, is their capability for parallelization.
Understanding Transformers provides a foundation for delving into more advanced topics in AI and machine learning. Many current research directions and innovations build upon the Transformer architecture, making it essential knowledge for staying up-to-date in the field. Further, the popularity of Transformers has led to a wealth of resources, including research papers, tutorials, open-source implementations (like Hugging Face’s Transformers library), and community support. This makes it easier to learn, experiment, and apply Transformer models in various projects.
2. Terminology
Transformers use a mechanism called attention to determine the importance of different words in a sequence. The core components of this attention mechanism are queries, keys, and values. Let’s take a closer look at some fundamental components of Transformers first and familiarize ourselves with some important concepts.
softmax
Softmax function is a mathematical function that converts a vector of values into a probability distribution. It is widely used in machine learning, especially in classification tasks and attention mechanisms, because it transforms input values to be in the range (0, 1) and ensures they sum up to 1. The softmax function is defined as follows:
\[\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}\]where:
- \(x_i\) is the \(i^{th}\) element of the input vector.
- \(e\) is the base of the natural logarithm.
and the denominator is the sum of the exponentials of all elements in the input vector. Here is a simple implementation in Python:
import numpy as np
def softmax(x):
e_x = np.exp(x)
return e_x / np.sum(e_x)
# Example input vector
input_vector = np.array([1.0, 2.0, 3.0])
# Compute softmax
softmax_output = softmax(input_vector)
print("Input Vector:", input_vector)
print("Softmax Output:", softmax_output)
which will return
Input Vector: [1. 2. 3.]
Softmax Output: [0.09003057 0.24472847 0.66524096]
Tokenization and Word Embedding
This is the process of breaking down a text into smaller units, which are called tokens. These tokens can be words, subwords, or characters. Tokenization is an important step in natural language processing because it transforms raw text data into a format that can be processed and converted into numerical format later (using embedding process).
Word embeddings are dense vector representations of words in a high-dimensional space, where similar words are closer to each other in this space. This is where we convert words into numerical format, which is essential for computing purposes. Here is a simple Python code to get a better sense of tokenization procedure:
import re
def simple_tokenize(text):
# Define a regular expression pattern for tokenization
pattern = re.compile(r'(\b\w+\b|[.,!?;])')
# Use findall to get all matches
tokens = pattern.findall(text)
return tokens
# Example text
text = "Hello, how are you doing today?"
# Tokenize the text
tokens = simple_tokenize(text)
print("Original Text:", text)
print("Tokens:", tokens)
with the output
Original Text: Hello, how are you doing today?
Tokens: ['Hello', ',', 'how', 'are', 'you', 'doing', 'today', '?']
Obviously, this approach is not efficient and practical for tokenizing large bodies of text, there are more practical approaches that basically tokenize the text using a vocabulary of possible tokens.
“In practice, a compromise between letters and full words is used, and the final vocabulary includes both common words and word fragments from which larger and less frequent words can be composed.” ~ Simon J.D. Prince, “Understanding Deep Learning”
To have a better understanding of how words can be represented using numbers, let’s take a look at the one-hot encoding procedure, where each word is represented as a sparse vector with a value of 1 in the position corresponding to the word’s index in the vocabulary and 0 elsewhere. Here is a simple Python code to achieve this for a given sentence:
def one_hot_encode(word, vocab):
# Create a dictionary to store one-hot encoded vectors
one_hot_vec = {}
for idx, w in enumerate(vocab):
one_hot_vec[w] = [1 if idx == i else 0 for i in range(len(vocab))]
# Return the one-hot encoded vector for the given word
return one_hot_vec.get(word, [0] * len(vocab))
# Example vocabulary
vocab = ["apple", "banana", "orange", "grape"]
# Example words to encode
words_to_encode = ["apple", "orange", "kiwi"]
# One-hot encode each word
for word in words_to_encode:
one_hot_vector = one_hot_encode(word, vocab)
print(f"One-hot vector for '{word}': {one_hot_vector}")
returning the following
One-hot vector for 'apple': [1, 0, 0, 0]
One-hot vector for 'orange': [0, 0, 1, 0]
One-hot vector for 'kiwi': [0, 0, 0, 0]
Now, let’s go back to the idea of word embedding. This is the process of mapping tokens to numerical vectors in a continuous vector space. This process also helps with semantic relationships and contextual meaning of words and subwords. There are various approaches to achieve this, including
- Count-Based Methods such as TF-IDF and Latent Semantic Analysis
- Prediction-Based Methods such as Word2Vec, GloVe, and FastText
- Contextual Embeddings such as ELMo, BERT, GPT
- Subword and Character-Level Embeddings such as Byte Pair Encoding (BPE), and Char-CNN, and Char-RNN
As an example, let’s take a look at the procedure for Byte Pair Encoding (BPE), which is a technique that merges commonly occurring sub-strings using the frequency of their occurrence. This process replaces the most frequent pair of bytes (or characters) in a sequence with a single, unused byte (or character). Let’s say we have a set of tokens [“low”, “lowest”, “newer”, “wider”].
- Step 1: We prepare the input by splitting each word into characters and adding a special end-of-word token
</w> - Step 2: We create a vocabulary that counts the frequency of each word in the input
- Step 3: We then calculate the frequencies of adjacent character pairs
- Step 4: Let’s say the most frequent pairs are (‘l’, ‘o’). We merge this pair in the vocabulary
- Step 5: We Update the vocabulary and recalculate pair frequencies And we can continue this process in the same manner…
After performing a number of merges, we obtain a vocabulary where common subword units are represented as single tokens. This reduces the vocabulary size and captures subword information that can help with out-of-vocabulary words.
Here is a python code that you can run to see how the process works:
import re
from collections import defaultdict
def get_stats(vocab):
"""
Given a vocabulary (dictionary mapping words to frequency counts), returns a dictionary of tuples representing the frequency count of pairs of characters
in the vocabulary.
"""
pairs = defaultdict(int)
for word, freq in vocab.items():
symbols = word.split()
for i in range(len(symbols)-1):
pairs[symbols[i],symbols[i+1]] += freq
return pairs
def merge_vocab(pair, v_in):
"""
Given a pair of characters and a vocabulary, returns a new vocabulary with the pair of characters merged together wherever they appear.
"""
v_out = {}
bigram = re.escape(' '.join(pair))
p = re.compile(r'(?<!\S)' + bigram + r'(?!\S)')
for word in v_in:
w_out = p.sub(''.join(pair), word)
v_out[w_out] = v_in[word]
return v_out
def get_vocab(data):
"""
Given a list of strings, returns a dictionary of words mapping to their frequency count in the data.
"""
vocab = defaultdict(int)
for line in data:
for word in line.split():
vocab[' '.join(list(word)) + ' </w>'] += 1
return vocab
def byte_pair_encoding(data, n):
"""
Given a list of strings and an integer n, returns a list of n merged pairs
of characters found in the vocabulary of the input data.
"""
vocab = get_vocab(data)
for i in range(n):
pairs = get_stats(vocab)
best = max(pairs, key=pairs.get)
print("-----")
print('most frequent pair:', best)
print('vocab before merge:',*vocab.items())
vocab = merge_vocab(best, vocab)
print('vocab after merge:', *vocab.items())
return vocab
# Example usage:
corpus = "low,lowest,newer,wider"
data = corpus.split(',')
num_merges = 5 # set the number of merging steps
bpe_pairs = byte_pair_encoding(data, num_merges)
for k,v in bpe_pairs.items():
print(k,v)
once run, this will return
-----
most frequent pair: ('l', 'o')
vocab before merge: ('l o w </w>', 1) ('l o w e s t </w>', 1) ('n e w e r </w>', 1) ('w i d e r </w>', 1)
vocab after merge: ('lo w </w>', 1) ('lo w e s t </w>', 1) ('n e w e r </w>', 1) ('w i d e r </w>', 1)
-----
most frequent pair: ('lo', 'w')
vocab before merge: ('lo w </w>', 1) ('lo w e s t </w>', 1) ('n e w e r </w>', 1) ('w i d e r </w>', 1)
vocab after merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w e r </w>', 1) ('w i d e r </w>', 1)
-----
most frequent pair: ('e', 'r')
vocab before merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w e r </w>', 1) ('w i d e r </w>', 1)
vocab after merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w er </w>', 1) ('w i d er </w>', 1)
-----
most frequent pair: ('er', '</w>')
vocab before merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w er </w>', 1) ('w i d er </w>', 1)
vocab after merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w er</w>', 1) ('w i d er</w>', 1)
-----
most frequent pair: ('low', '</w>')
vocab before merge: ('low </w>', 1) ('low e s t </w>', 1) ('n e w er</w>', 1) ('w i d er</w>', 1)
vocab after merge: ('low</w>', 1) ('low e s t </w>', 1) ('n e w er</w>', 1) ('w i d er</w>', 1)
-- Final vocab:
low</w> 1
low e s t </w> 1
n e w er</w> 1
w i d er</w> 1
Once you have your vocabulary vector from an operation like BPE, you then use that to map your tokens for an input text to some index.
For example, let’s say you end up having a vocabulary with the following index values for the tokens:
| Token | The | cat | sat | on | the | mat |
|---|---|---|---|---|---|---|
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
so for an input text “The cat sat” with tokenization [“The”, “cat”, “sat”], you ended up having a token-to-index mapping [0,1,2].
Let’s assume that your embedding matrix, \(E\), is a matrix where each row corresponds to the embedding vector of a token in the vocabulary. Let’s assume the embeddings are 3-dimensional, i.e. I can show each embedding with a vector with three components in the vector space. I am also going to assume some random values for the entries. Keep in mind that the embedding matrix \(E\) is typically learned during the training of the model.
\[E=\begin{bmatrix} 0.1 & 0.2 & 0.3 & -> (\text{embedding for ''The''})\\ 0.4 & 0.5 & 0.6 & -> (\text{embedding for ''cat''})\\ 0.7 & 0.8 & 0.9 & -> (\text{embedding for ''sat''})\\ 0.1 & 0.3 & 0.5 & -> (\text{embedding for ''on''})\\ 0.2 & 0.4 & 0.6 & -> (\text{embedding for ''the''})\\ 0.3 & 0.5 & 0.7 & -> (\text{embedding for ''mat''})\\ \end{bmatrix}\]then, we can look up the corresponding rows in the embedding matrix \(E\) given the indices [0,1,2] for the input matrix (\(X\)). Therefore, our input matrix for the model becomes:
\[X=\begin{bmatrix} 0.1 & 0.2 & 0.3 \\ 0.4 & 0.5 & 0.6 \\ 0.7 & 0.8 & 0.9 \\ \end{bmatrix}\]Hopefully this makes the idea of tokenization, embedding matrix, and their relationship to the input sequence very clear. Let’s talk about queries, keys, and values next.
Queries, Keys, and Values
Quesries are vectors that represent the word (or token) for which we want to compute the attention score. Essentially, they are the questions we are asking about the importance of other words. Keys are vectors that represent the words in the context we are considering. They act like an index or a reference. Values are the actual word embeddings or features that we use to generate the output. They contain the information we are interested in.
So at this point, knowing the tokens, we can implement some form of linear transformation with some given weights in the transformation matrices (which they need to be calculated during the training process) to find the queries, keys, and values as follows (Don’t worry too much about what they mean. Juts get a sense of how they can be calculated from input word embeddings. Things become more clear moving forward.)
\[Q_i=W_Q\times x_i \quad, \quad K_i=W_K\times x_i \quad , \quad V_i=W_V\times x_i\]Here, \(x_i\) is the vector space for each token, i.e. each row in Matrix \(X\) (in previous section) and \(W\)’s are weight matrices that need to be found during the training. Also,
\[Q_i=[q_1, q_2, q_3, ...] \quad , \quad K_i=[k_1, k_2, k_3, ...] \quad, \quad \text{and} \quad V_i=[v_i, v_2, v_3,...]\]where \(q_i\), \(k_i\), and \(v_i\) are each a vector.
This matrix representation is basically telling you that you will have one query vector, one key vector, and one value vector for each word embedding vector. In another word, now we have three vector representations for each word embedding vector.
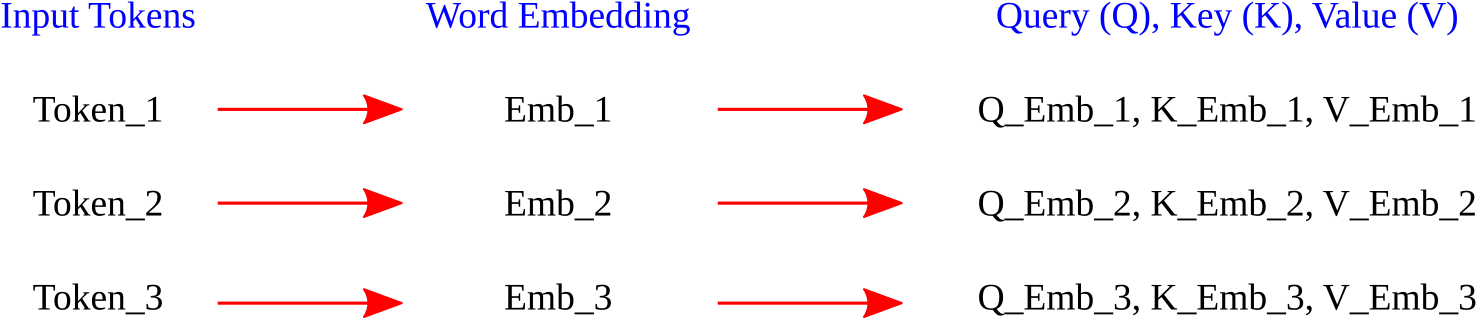
Self-Attention Mechanism
This mechanism calculates a score between each query and every key to determine how much weight should be given to each word. This weight is usually computed as a dot product of the query and key vectors. We typically apply a softmax to the outcome to keep things under control!
\[\text{Attention Weights}=Softmax[K^TQ]\]The weighted values are then calculated using
\[\text{Weighted Values}=V.Softmax[K^TQ]\]Let me try to put everything together so you can get a better picture of the general procedure for the case of an input with three tokens:

So at this point, the output for each token incorporates information from all other tokens in the sequence, weighted by their relevance. This means that the representation of token \(i\) is not just based on the token itself but it is also influenced by how much attention it gives to other tokens.
NOTE: In order to deal with large magnitudes in the dot product operation, when calculating the weights, we typically scale the dot product as \(\text{Weighted Values}=V.Softmax[\frac{K^TQ}{\sqrt{D_q}}]\), where \(D_q\) is the dimension of the queries. This scaling procedure when dealing with large magnitudes in attention computation is important since
“Small changes to the inputs to the softmax function might have little effect on the output (i.e. the gradients are very small), making the model difficult to train”. ~ Simon J.D. Prince, “Understanding Deep Learning”
We can also write a simple Python code for this procedure and test it out:
import numpy as np
d_k = 3 # Dimension of queries and keys
d_v = 3 # Dimension of values
# Example word representations (for simplicity, these are random)
queries = np.array([[1, 0, 1], [0, 1, 0], [1, 1, 0]]) # 3 words, d_k dimensions
keys = np.array([[1, 1, 1], [0, 1, 0], [1, 0, 1]]) # 3 words, d_k dimensions
values = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 3 words, d_v dimensions
# Calculating the dot product between queries and keys (transpose keys)
dot_products = np.dot(queries, keys.T)
print("Dot Products:\n", dot_products)
# Applying softmax to get attention weights
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
attention_weights = softmax(dot_products)
print("Attention Weights:\n", attention_weights)
# Multiplying the attention weights with the values
weighted_values = np.dot(attention_weights, values)
print("Output:\n", weighted_values)
returning
Attention Weights:
[[0.46831053 0.06337894 0.46831053]
[0.4223188 0.4223188 0.1553624 ]
[0.57611688 0.21194156 0.21194156]]
Weighted Values:
[[4. 5. 6. ]
[3.19913082 4.19913082 5.19913082]
[2.90747402 3.90747402 4.90747402]]
If things are still not clear, take a look at the Attention Mechanism: Learn by Example section, where I went through this procedure with an example calculations for a few tokens in a given sentence.
Normalization
This mechanism, like Batch Normalization, is commonly used in neural networks to stabilize and accelerate the training process. The idea is to normalize the input of each layer so that it has a mean of zero and a variance of one. This helps in mitigating the internal covariate shift problem. Here is how Batch Normalization works:
- Calculate Mean and Variance: For a given batch, calculate the mean and variance of the inputs.
- Normalize: Subtract the mean and divide by the standard deviation to normalize the inputs.
- Scale and Shift: Apply learned scaling and shifting parameters to the normalized inputs.
Positional Encoding
Positional encoding provides information about the position of each word in the sequence. This is essential because unlike recurrent or convolutional layers, transformers do not have a built-in notion of sequence order.
Positional encodings are added to the input embeddings to give the model some information about the relative or absolute position of the tokens. The encoding matrix can be created by hand or can be learned. It can be added to the network inputs or at every network layer.
One common approach is to use sine and cosine functions of different frequencies. The idea is to generate unique positional encodings that the model can learn to interpret.
For even indices:
\[\text{PE}_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)\]For the odd indices:
\[\text{PE}_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)\]where
- \(pos\) is the position in the sequence,
- \(i\) is the dimension,
- \(d_{model}\) is the dimension of the model, i.e. size of the vector space in which the tokens are represented.
Here’s a simple implementation of positional encoding in Python:
import numpy as np
import matplotlib.pyplot as plt
scaling_factor = 10000
def positional_encoding(max_len, d_model):
pos_enc = np.zeros((max_len, d_model))
for pos in range(max_len):
for i in range(0, d_model, 2):
pos_enc[pos, i] = np.sin(pos / (scaling_factor ** ((2 * i)/d_model)))
pos_enc[pos, i + 1] = np.cos(pos / (scaling_factor ** ((2 * i)/d_model)))
return pos_enc
# Example usage
max_len = 10 # Maximum length of the sequence
d_model = 6 # Dimension of the model
pos_encoding = positional_encoding(max_len, d_model)
print("Positional Encoding Matrix:\n", pos_encoding)
# Visualize the positional encoding
plt.figure(figsize=(10, 6))
plt.pcolormesh(pos_encoding, cmap='viridis')
plt.xlabel('Depth')
plt.xlim((0, d_model))
plt.ylabel('Position')
plt.colorbar()
plt.title('Positional Encoding')
plt.show()
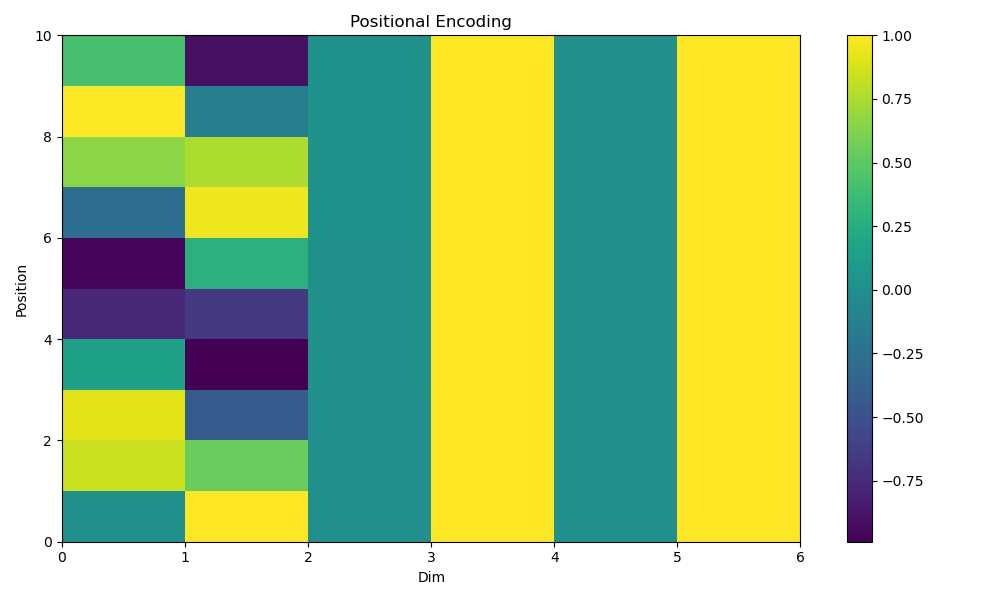
In the output figure, you can see that for any given position across the dimensions, we have a unique set of color combination.
3. Attention Mechanism: Learn by Example
In this section, I will try to focus on detailed calculations for the attention mechanism, hoping that it might help those who are more comfortable with actually seeing sample calculations when it comes to understanding a concept. Let’s use the following sentence:
Despite the heavy rain, the children played happily in the park, unaware of the approaching storm.
Tokenization
First, let’s tokenize the sentence into individual words or subwords:
Tokens=[ “Despite”, “the” , “heavy” , “rain”, “,” , “the” , “children” , “played” , “happily” , “in” , “the” , “park” , “,” , “unaware” , “of” , “the” , “approaching” , “storm” , “.” ]
Embedding
We then map the tokens into a vector in a high-dimensional space. This mapping is achieved using a pre-trained embedding matrix (e.g., Word2Vec, GloVe, or embeddings learned as part of a transformer model like BERT or GPT).
Let’s use a simplified example where each token is mapped to a 4-dimensional vector. In practice, these vectors would be of higher dimensions (e.g., 300, 768, 1024).
Here’s an example of what this might look like (with randomly chosen values for illustration):
"Despite"→[0.2,−0.1,0.5,0.3]
"the"→[0.1,0.0,−0.1,0.4]
"heavy"→[−0.3,0.8,0.1,0.2]
"rain"→[0.4,0.3,−0.2,0.1]
","→[0.0,0.0,0.0,0.0]
"children"→[0.5,0.2,0.6,−0.1]
"played"→[0.3,0.1,0.4,0.7]
"happily"→[−0.2,0.5,−0.3,0.4]
"in"→[0.1,−0.3,0.2,0.5]
"park"→[0.4,0.6,0.1,−0.4]
"unaware"→[0.2,0.7,−0.5,0.1]
"of"→[0.1,0.0,0.3,−0.2]
"approaching"→[0.3,0.4,0.6,0.2]
"storm"→[0.5,−0.1,0.4,0.3]
"."→[0.0,0.0,0.0,0.0]
These vectors (embeddings) are typically learned from large corpora of text and capture semantic meanings. For example, “rain” and “storm” might have similar embeddings because they both relate to weather.
Building the Embedding Matrix
For our sentence, we create an embedding matrix where each row corresponds to the embedding of a token. If our sentence has 19 tokens and each token is embedded in a 4-dimensional space, our embedding matrix $E$ would be of size \(19\times4\):
| Token | Dimension 1 | Dimension 2 | Dimension 3 | Dimension 4 |
|---|---|---|---|---|
| Despite | 0.2 | -0.1 | 0.5 | 0.3 |
| the | 0.1 | 0.0 | -0.1 | 0.4 |
| heavy | -0.3 | 0.8 | 0.1 | 0.2 |
| rain | 0.4 | 0.3 | -0.2 | 0.1 |
| , | 0.0 | 0.0 | 0.0 | 0.0 |
| children | 0.5 | 0.2 | 0.6 | -0.1 |
| played | 0.3 | 0.1 | 0.4 | 0.7 |
| happily | -0.2 | 0.5 | -0.3 | 0.4 |
| in | 0.1 | -0.3 | 0.2 | 0.5 |
| the | 0.1 | 0.0 | -0.1 | 0.4 |
| park | 0.4 | 0.6 | 0.1 | -0.4 |
| unaware | 0.2 | 0.7 | -0.5 | 0.1 |
| of | 0.1 | 0.0 | 0.3 | -0.2 |
| the | 0.1 | 0.0 | -0.1 | 0.4 |
| approaching | 0.3 | 0.4 | 0.6 | 0.2 |
| storm | 0.5 | -0.1 | 0.4 | 0.3 |
| . | 0.0 | 0.0 | 0.0 | 0.0 |
Queries, Keys, and Values
For illustration purposes, let’s define our weight matrices with arbitrary values
\[W_Q=\begin{bmatrix} 0.1 & 0.2 & 0.3 & 0.4\\ 0.5 & 0.6 & 0.7 & 0.8\\ 0.9 & 1.0 & 1.1 & 1.2\\ 1.3 & 1.4 & 1.5 & 1.6 \end{bmatrix}\] \[W_K=\begin{bmatrix} 1.6 & 1.5 & 1.4 & 1.3\\ 1.2 & 1.1 & 1.0 & 0.9\\ 0.8 & 0.7 & 0.6 & 0.5\\ 0.4 & 0.3 & 0.2 & 0.1 \end{bmatrix}\] \[W_V=\begin{bmatrix} 0.1 & -0.2 & 0.3 & -0.4\\ -0.5 & 0.6 & -0.7 & 0.8\\ 0.9 & -1.0 & 1.1 & -1.2\\ -1.3 & 1.4 & -1.5 & 1.6 \end{bmatrix}\]and use them to calculate queries, keys, and values for the first three tokens
- “Despite” with embedding [0.2, −0.1, 0.5, 0.3]:
- “the” with embedding [0.1, 0.0, −0.1, 0.4] and “heavy” with embedding [−0.3, 0.8, 0.1, 0.2]:
By applying the learned weight matrices $W_Q$, $W_K$, and $W_V$, we transform the original embeddings into queries, keys, and values. These vectors are then used in the attention mechanism to compute attention scores and to derive contextually rich representations of each token. Let’s see how this works.
Computing Attention Weights
For each token, we compute the dot product of its query vector with the key vectors of all tokens. This results in the attention scores for each token relative to every other token.
Let’s continue with the example of “Despite” with
\[Q_{Despite}=\begin{bmatrix} 0.27 \\ 0.63 \\ 0.99 \\ 1.35\end{bmatrix}\]and then find the attention scores between “Despite” and three other tokens, including itself (“the”, “heavy”, and “Despite” ) with
\[K_{the}=\begin{bmatrix} 0.54 \\ 0.38 \\ 0.22 \\ 0.06\end{bmatrix} \quad , \quad K_{heavy}=\begin{bmatrix} 1.12 \\ 0.8 \\ 0.48 \\ 0.16\end{bmatrix} \quad , \quad K_{Despite}=\begin{bmatrix} 1.26 \\ 0.9 \\ 0.54 \\ 0.18\end{bmatrix}\]- Dot product between “Despite” and “the”: \(Dot(Q_{Despite}, K_{the})= 0.1458 + 0.2394 + 0.2178 + 0.081 = 0.684\)
- Dot product between “Despite” and “heavy”: \(Dot(Q_{Despite}, K_{heavy})= 0.3024 + 0.504 + 0.4752 + 0.216 = 1.4976\)
- Dot product between “Despite” and “Despite” (self-attention): \(Dot(Q_{Despite}, K_{Despite})= 0.3402 + 0.567 + 0.5346 + 0.243 = 1.6848\)
These dot products represent the raw attention weights for “Despite” in relation to “the”, “heavy,” and itself.
\[\text{Softmax}([0.684, 1.4976, 1.6848]) = \left[ \frac{e^{0.684}}{e^{0.684} + e^{1.4976} + e^{1.6848}}, \frac{e^{1.4976}}{e^{0.684} + e^{1.4976} + e^{1.6848}}, \frac{e^{1.6848}}{e^{0.684} + e^{1.4976} + e^{1.6848}} \right]\]These softmax values represent the normalized attention scores for “Despite” with respect to “the,” “heavy,” and itself, respectively. They indicate the relative importance of “Despite” compared to the other tokens during the attention mechanism.
4. Transformer Models
We can generally classify transformers into three models, Encoders, Decoders, and Encoder-Decoders. An encoder:
“…transforms the text embeddings into a representation that can support variety of tasks.” ~ Simon J.D. Prince, “Understanding Deep Learning”
A decoder, however, is typically used to generate the next output and to continue the given input text, like GPT models.
Finally, encoder-decoders are implemented in
“…sequence-to-sequence tasks, where one text string is converted into another.” ~ Simon J.D. Prince, “Understanding Deep Learning”
A common example for encoder-decoder model is language translation.
5. Coding a Simple Transformer
In this section, we will try to develop a simple transformer piece-by-piece using Python. This simple model includes an embedding layer, positional encoding, attention mechanism, a feed-forward neural network, normalization layer, as well as encoder and decoder parts. Keep in mind that a typical Transformer has a much more complex structure with a extra components (such as residual connections and masked attention) and it also is implemented through a multi-headed approach for parallel computation. Here, the goal is to have a better understanding of how the building blocks of a Transformer piece together.
Embedding Layer
Let’s start with the embedding layer.
import numpy as np
class EmbeddingLayer:
def __init__(self, vocab_size, d_model):
self.embedding_matrix = np.random.rand(vocab_size, d_model)
def __call__(self, x):
return self.embedding_matrix[x]
Here, we use a simple example, the sentence “I love learning from examples” with a given vocabulary, and see how this embedding layer works:
# Defining the vocabulary and input sentence
vocab = {"I": 0, "love": 1, "learning": 2, "from": 3, "examples": 4}
input_sentence = ["I", "love", "learning"]
# Converting the input sentence to indices
input_indices = [vocab[word] for word in input_sentence]
# Initializing the embedding layer
vocab_size = len(vocab)
d_model = 4 # Let's use 4 dimensions for simplicity
embedding_layer = EmbeddingLayer(vocab_size, d_model)
# Getting the embeddings for the input indices
embeddings = embedding_layer(np.array(input_indices))
print("Input Indices:", input_indices)
print("Embeddings:\n", embeddings)
The above code will give the following output (yours will be different since I used np.random.rand in the EmbeddingLayer class so every run gives a different set of outputs):
Input Indices: [0, 1, 2]
Embeddings:
[[0.90034368 0.82241612 0.02018069 0.62033932]
[0.6351551 0.33107626 0.78112305 0.21081683]
[0.93584476 0.08042298 0.05619254 0.74456291]]
Positional Encoding
We continue our model development by creating a positional encoding layer:
class PositionalEncoding:
def __init__(self, d_model, max_len=5000):
self.encoding = np.zeros((max_len, d_model))
position = np.arange(0, max_len)[:, np.newaxis]
div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))
self.encoding[:, 0::2] = np.sin(position * div_term)
self.encoding[:, 1::2] = np.cos(position * div_term)
def __call__(self, x):
seq_len = x.shape[1]
return x + self.encoding[:seq_len, :]
Here is the implementation of the class using the example sentence in the previous section:
pos_encoding_layer = PositionalEncoding(d_model)
embeddings_with_positional_encoding = pos_encoding_layer(embeddings[np.newaxis, :])
print("Embeddings with Positional Encoding:\n", embeddings_with_positional_encoding)
which will return (yours will be different since I used np.random.rand in the EmbeddingLayer class so every run gives a different set of outputs)
Embeddings with Positional Encoding:
[[[ 0.90034368 1.82241612 0.02018069 1.62033932]
[ 1.47662609 0.87137857 0.79112288 1.21076683]
[ 1.84514219 -0.33572386 0.07619121 1.74436292]]]
In the output, the positional encoding are those same vectors as embeddings with positional information added. The positional encoding modifies the embeddings to incorporate the position of each word in the sentence, making it easier for the model to learn the order of words.
Self-Attention Mechanism
Once we have our embeddings, we need to have our self attention layer, which can be coded as follows
class SelfAttention:
def __init__(self, d_model):
self.d_model = d_model
self.W_q = np.random.rand(d_model, d_model)
self.W_k = np.random.rand(d_model, d_model)
self.W_v = np.random.rand(d_model, d_model)
self.W_o = np.random.rand(d_model, d_model)
def __call__(self, x):
Q = np.dot(x, self.W_q)
K = np.dot(x, self.W_k)
V = np.dot(x, self.W_v)
scores = np.dot(Q, K.T) / np.sqrt(self.d_model)
attention_weights = np.exp(scores) / np.sum(np.exp(scores), axis=-1, keepdims=True)
attention_output = np.dot(attention_weights, V)
return np.dot(attention_output, self.W_o)
Again, let us look at how it operates using a simple example, assuming a sentence with 3 tokens, for a 4-dimensional model
# A simple input matrix (3 words with 4-dimensional embeddings)
input_matrix = np.array([[1, 0, 1, 0], [0, 1, 0, 1], [1, 1, 1, 1]])
d_model = 4 # Dimensionality of the input
self_attention_layer = SelfAttention(d_model)
output_matrix = self_attention_layer(input_matrix)
print("Input Matrix:\n", input_matrix)
print("Output Matrix after Self-Attention:\n", output_matrix)
The above input example will return (yours will be different since I used np.random.rand in the EmbeddingLayer class so every run gives a different set of outputs)
Input Matrix:
[[1 0 1 0]
[0 1 0 1]
[1 1 1 1]]
Output Matrix after Self-Attention:
[[4.00438965 3.73163309 4.01682177 3.50892256]
[4.08366923 3.80766097 4.10031155 3.5832559 ]
[4.37889227 4.08744366 4.40506536 3.85251859]]
In the output, the input matrix represents three words with four features each. And the output matrix shows the result of applying the self-attention mechanism to the input matrix, essentially showing how each word’s representation is influenced by the others in the sequence.
We need two more layers, one fully-connected feed-forward neural network and one normalization layer.
Feed-Forward Neural Network
This layer is just a typical fully connected neural network. The purpose of the feed-forward network is to transform the attention output.
The ReLU activation introduces non-linearity, allowing the model to learn more complex patterns and representations beyond what linear transformations can capture. Further, this layer can help capture richer features and improve the model’s ability to generalize. Finally, this layer allows the model to process each token’s representation separately after attending to other tokens, enhancing the model’s capacity to learn individual token features.
class FeedForward:
def __init__(self, d_model, d_ff):
# d_model: dimension of the input and output (same as the input embedding dimension).
# d_ff: dimension of the hidden layer in the feedforward network.
# A weight matrix of shape `(d_model, d_ff)` initialized with random values.
self.W1 = np.random.rand(d_model, d_ff)
# A weight matrix of shape `(d_ff, d_model)` initialized with random values.
self.W2 = np.random.rand(d_ff, d_model)
def __call__(self, x):
# `np.maximum(0, np.dot(x, self.W1))`: applies the ReLU activation function to introduce non-linearity.
# `np.dot(np.maximum(0, np.dot(x, self.W1)), self.W2)`: projects the hidden layer back to the original dimension `d_model`.
return np.dot(np.maximum(0, np.dot(x, self.W1)), self.W2)
Layer Normalization
The LayerNorm class implements layer normalization. The layer normalization is applied to the inputs of the sub-layers in the Transformer architecture to stabilize and accelerate the training process. In the transformer architecture, layer normalization is applied at various points, typically before and after the main sub-layers (self-attention and feed-forward neural network).
class LayerNorm:
def __init__(self, d_model, eps=1e-6):
self.eps = eps
self.gamma = np.ones(d_model)
self.beta = np.zeros(d_model)
def __call__(self, x):
mean = np.mean(x, axis=-1, keepdims=True)
std = np.std(x, axis=-1, keepdims=True)
return self.gamma * (x - mean) / (std + self.eps) + self.beta
Encoder Layer
Now, putting all these components together, we can define a simple Encoder structure as follows:
class EncoderLayer:
def __init__(self, d_model, d_ff):
self.self_attention = SelfAttention(d_model)
self.feed_forward = FeedForward(d_model, d_ff)
self.layer_norm1 = LayerNorm(d_model)
self.layer_norm2 = LayerNorm(d_model)
def __call__(self, x):
attn_output = self.self_attention(x)
x = self.layer_norm1(x + attn_output)
ff_output = self.feed_forward(x)
x = self.layer_norm2(x + ff_output)
return x
And here is an example code to test the procedure:
# Simple example input matrix (3 words with 4-dimensional embeddings)
input_matrix = np.array([[1.0, 0.5, 0.0, 0.2], [0.4, 0.7, 0.1, 0.8], [0.6, 0.1, 0.9, 0.3]])
d_model = 4 # Dimension of the input
d_ff = 8 # Dimension of the hidden layer in the feedforward network
encoder_layer = EncoderLayer(d_model, d_ff)
# Applying the EncoderLayer to the input matrix
output_matrix = encoder_layer(input_matrix)
print("Input Matrix:\n", input_matrix)
print("Output Matrix after EncoderLayer:\n", output_matrix)
The final output matrix (output_matrix) contains the transformed embeddings of the input tokens. Each row in this matrix represents a token in the sequence, but now these token representations are context-aware and enriched with information from the entire sequence.
The potential applications of the output are
- Context-Awareness: Each token’s representation in the output matrix is affected by other tokens in the sequence, capturing some of the dependencies and relationships.
- Foundation for Further Processing: This output serves as the input for subsequent layers in the Transformer model, building progressively richer representations that can be used for tasks like translation, classification, or other sequence-to-sequence tasks.
Decoder Layer
We can also construct a Decoder using the concepts and codes we previously introduced:
class DecoderLayer:
def __init__(self, d_model, d_ff):
self.self_attention = SelfAttention(d_model)
self.enc_dec_attention = SelfAttention(d_model)
self.feed_forward = FeedForward(d_model, d_ff)
self.layer_norm1 = LayerNorm(d_model)
self.layer_norm2 = LayerNorm(d_model)
self.layer_norm3 = LayerNorm(d_model)
def __call__(self, x, enc_output):
# Self-attention on the decoder's own input
self_attn_output = self.self_attention(x)
x = self.layer_norm1(x + self_attn_output)
# Cross-attention with the encoder's output
enc_dec_attn_output = self.enc_dec_attention(x)
x = self.layer_norm2(x + enc_dec_attn_output)
# Feedforward network
ff_output = self.feed_forward(x)
x = self.layer_norm3(x + ff_output)
return x
Here, there is a new concept called Cross-Attention (or encoder-decoder attention).
Remember that a Transformer pays attention to various tokens in a given sentence using self-attention mechanism. However, when we have a decoder, paying attention to the tokens in a sentence in the decoder is not enough, we also need to pay attention to the encoder’s outputs. For instance in a language translation procedure, when we couple an encoder with a decoder, the model needs to pay attention to the words in the translated sentence in the output language (self-attention) and the words in the original language (cross-attention). Therefore, using this cross-attention layer, decoder embeddings attend to the encoder embeddings. In this scenario,
“… the queries are computed from the decoder embeddings and the keys and values from the encoder embeddings.” ~ Simon J.D. Prince, “Understanding Deep Learning”
Let us then take a look at a simple example of a decoder along with an example of how it takes a set of inputs and returns an output which is a final transformed matrix, capturing the relationships between the decoder’s input tokens and the encoder’s output tokens. This matrix is then can be passed to the next layer of the Transformer decoder or to be used for generating the output sequence.
Putting it all together with an example:
import numpy as np
class SelfAttention:
def __init__(self, d_model):
self.d_model = d_model
self.W_q = np.random.rand(d_model, d_model)
self.W_k = np.random.rand(d_model, d_model)
self.W_v = np.random.rand(d_model, d_model)
self.W_o = np.random.rand(d_model, d_model)
def __call__(self, x):
Q = np.dot(x, self.W_q)
K = np.dot(x, self.W_k)
V = np.dot(x, self.W_v)
scores = np.dot(Q, K.T) / np.sqrt(self.d_model)
attention_weights = np.exp(scores) / np.sum(np.exp(scores), axis=-1, keepdims=True)
attention_output = np.dot(attention_weights, V)
return np.dot(attention_output, self.W_o)
class FeedForward:
def __init__(self, d_model, d_ff):
self.W1 = np.random.rand(d_model, d_ff)
self.W2 = np.random.rand(d_ff, d_model)
def __call__(self, x):
return np.dot(np.maximum(0, np.dot(x, self.W1)), self.W2)
class LayerNorm:
def __init__(self, d_model, eps=1e-6):
self.eps = eps
self.gamma = np.ones(d_model)
self.beta = np.zeros(d_model)
def __call__(self, x):
mean = np.mean(x, axis=-1, keepdims=True)
std = np.std(x, axis=-1, keepdims=True)
return self.gamma * (x - mean) / (std + self.eps) + self.beta
class DecoderLayer:
def __init__(self, d_model, d_ff):
self.self_attention = SelfAttention(d_model)
self.enc_dec_attention = SelfAttention(d_model)
self.feed_forward = FeedForward(d_model, d_ff)
self.layer_norm1 = LayerNorm(d_model)
self.layer_norm2 = LayerNorm(d_model)
self.layer_norm3 = LayerNorm(d_model)
def __call__(self, x, enc_output):
# Self-attention on the decoder's own input
self_attn_output = self.self_attention(x)
x = self.layer_norm1(x + self_attn_output)
# Cross-attention with the encoder's output
enc_dec_attn_output = self.enc_dec_attention(x)
x = self.layer_norm2(x + enc_dec_attn_output)
# Feedforward network
ff_output = self.feed_forward(x)
x = self.layer_norm3(x + ff_output)
return x
# Example input matrix (decoder's input)
decoder_input = np.array([[0.1, 0.2, 0.3, 0.4],
[0.5, 0.6, 0.7, 0.8],
[0.9, 1.0, 1.1, 1.2]])
# Example encoder output matrix
encoder_output = np.array([[1.0, 0.9, 0.8, 0.7],
[0.6, 0.5, 0.4, 0.3],
[0.2, 0.1, 0.0, -0.1]])
d_model = 4 # Dimensionality of the input
d_ff = 8 # Dimensionality of the hidden layer in the feedforward network
decoder_layer = DecoderLayer(d_model, d_ff)
output_matrix = decoder_layer(decoder_input, encoder_output)
print("Decoder Input Matrix:\n", decoder_input)
print("Encoder Output Matrix:\n", encoder_output)
print("Output Matrix after DecoderLayer:\n", output_matrix)
6. Final Comments
The main place to experiment with various Transformer-based models, used for NLP, Computer Vision, and automatic speech recognition is the Hugging Face. I strongly suggest joining the community and learn by following tutorials and implementing models for your own projects.
To have a much better understanding of how the mechanics of Transformers for NLP-related tasks work along with learning how to implement various NLP-related tasks, I suggest looking at Andrej Karpathy YouTube channel, specially Let’s build GPT: from scratch, in code, spelled out. and Let’s reproduce GPT-2 (124M).
If you are looking for more comprehensive and clear discussion about Transformers and their working principles, I suggest Deep Learning: Foundations and Concepts by Christopher M. Bishop and Hugh Bishop (chapter 12) and also Understanding Deep Learning by Simon J.D. Prince (chapter 12).
Enjoy Reading This Article?
Here are some more articles you might like to read next: