Dynamic Mode Decomposition for Fluid Dynamics

Author’s Note: This post is based on a class project that I assigned to students in the Data-Driven Problem Solving course, which I taught in the Mechanical Engineering Department at the Cooper Union for the Advancement of Science and Art in Fall 2024. You can download the data for this post from this link.

Theoretical Background

Before we dive into the specifics of SVD and DMD, let’s understand why we need these data-driven modeling techniques:

1. Complex Systems: Many real-world systems, like fluid flows, are incredibly complex. Traditional physics-based models can be too complicated or computationally expensive to solve.

2. Data Abundance: We often have lots of data from sensors or simulations, but we need ways to make sense of it all.

3. Pattern Discovery: Data-driven methods can help us find hidden patterns or structures in our data that we might not see otherwise.

4. Prediction: Once we understand the patterns, we can use them to make predictions about how the system will behave in the future.

5. Simplification: These methods can help us simplify complex systems, focusing on the most important aspects.

Now, let’s look at a powerful data-driven modeling techniques: Dynamic Mode Decomposition (DMD). First, we look at Singular Value Decomposition (SVD) concept and then expand that to DMD.

Singular Value Decomposition (SVD)

Think of SVD as a way to break down a complicated puzzle into simpler pieces.

1. What it does: SVD takes a big, complex matrix (like a puzzle) and breaks it into three simpler matrices.

2. The Math: If A is our data matrix, SVD says we can write it as:

   A = U * Σ * V^T

   Where:

   • U and V are like the puzzle’s edge pieces and corner pieces
   • Σ (Sigma) is like the importance of each piece

3. Simple Example: Imagine you have data about students’ heights and weights. SVD might show you that there’s one main pattern (taller students tend to weigh more) and some smaller patterns.

4. Why it’s useful:

   • It helps us find the most important patterns in our data.
   • We can use it to reduce noise in our data.
   • It’s a key step in many other techniques, including DMD.

If you want to get a better understading of the concept of SVD, I strongly recommend reading this short post and then watching these two, videos explaining the applications and mathematical derivation: - Singular Value Decomposition (SVD): Overview - Singular Value Decomposition (SVD): Mathematical Overview

If you want to dive deeper, here is another video that I suggest watching, which requires some background in linear algebra and matrix operations.

Dynamic Mode Decomposition (DMD)

DMD is like a video editor for your data, helping you find repeating patterns over time.

1. What it does: DMD looks at how your system changes over time and tries to find the main “actors” (modes) and their “scripts” (how they change).

2. The Math: If we have a series of data snapshots X₁, X₂, X₃, …, DMD assumes there’s some matrix A such that:

   X₂ ≈ A * X₁

   X₃ ≈ A * X₂

   And so on…

3. Simple Example: Imagine watching waves on a beach. DMD might find that there’s a big, slow wave (one mode) and smaller, faster ripples (other modes).

4. How it works:
   1. We arrange our data into two matrices: X₁ (earlier times) and X₂ (later times)
   2. We use SVD on X₁ to break it down: X₁ = U * Σ * V^T
   3. We use this to find our A matrix: A ≈ X₂ * V * Σ⁻¹ * U^T
   4. The eigenvectors of A are our modes, and the eigenvalues tell us how these modes change over time
5. Why it’s useful:
   • It can find patterns that repeat over time.
   • It can help us predict future behavior.
   • It works well even with complex, nonlinear systems.

If you want to know more about DMD, I suggest watching this video. However, keep in mind that the complete understanding requires some background in linear algebra.

Putting It All Together

Imagine you’re studying a river (our complex system). You take many photos over time (your data). SVD helps you identify the main features of the river (like bends or rapids). DMD then shows you how these features change over time (like how water flows around a bend). With this information, you can better understand the river’s behavior and even predict how it might change in the future.

These techniques allow us to make sense of complex systems using data, even when we don’t fully understand all the underlying physics. They’re powerful tools in many fields, from fluid dynamics to finance to neuroscience.

DMD Analysis of 2D Fluid Flow Around a Cylinder

In this post, we’ll apply DMD to model the fluid flow around a cylinder in 2D, a classic problem in fluid dynamics. By the end of this post, you’ll have implemented DMD from scratch and gained insights into how it can be used to analyze fluid flow patterns.

Step 1: Data Preparation

In this step, we’ll prepare the data for our DMD analysis. We’ll use a pre-generated dataset of fluid flow around a cylinder.

Task 1.1: Load and Explore the Data

First, we write a function to load the fluid flow data and explore its basic properties. This step is crucial for understanding the structure of our data before we apply DMD.

import numpy as np
import matplotlib.pyplot as plt

def load_fluid_flow_data(file_path):
    """
    Load fluid flow data from a file and return it as a numpy array.
    
    Parameters:
    file_path (str): Path to the data file
    
    Returns:
    np.array: 3D array of shape (n_timesteps, n_x, n_y) containing fluid flow data
    """
    # Your code here
    pass

def load_fluid_flow_data(file_path):
    """
    Load fluid flow data from a file and return it as a numpy array.
    Parameters:
    file_path (str): Path to the data file
    Returns:
    np.array: 3D array of shape (n_timesteps, n_x, n_y) containing fluid flow data
    """
    try:
        data = np.load(file_path)
        if data.ndim != 3:
            raise ValueError("Expected 3D array, but got array with {} dimensions".format(data.ndim))
        return data
    except FileNotFoundError:
        print(f"Error: File not found at {file_path}")
        return None
    except Exception as e:
        print(f"Error loading data: {str(e)}")
        return None

def plot_flow_field(flow_data, timestep):
    """
    Plot the flow field at a given timestep.
    NOTE:
        - use imshow from matplotlib library
        - use extent=[-2, 4, -1, 1] and aspect='equal' options in your imshow plot to get better visulizations


    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    timestep (int): Timestep to plot
    """
    # Your code here
    pass

def plot_flow_field(flow_data, timestep):
    """
    Plot the flow field at a given timestep.
    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    timestep (int): Timestep to plot
    """
    plt.figure(figsize=(10, 8))
    plt.imshow(flow_data[timestep], cmap='viridis', extent=[-2, 4, -1, 1])
    plt.colorbar(label='Flow Magnitude')
    plt.title(f'Flow Field at Timestep {timestep}')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.show()

Try the following code to test the functions.

data = load_fluid_flow_data('cylinder_flow_data.npy')
plot_flow_field(data, timestep=0)

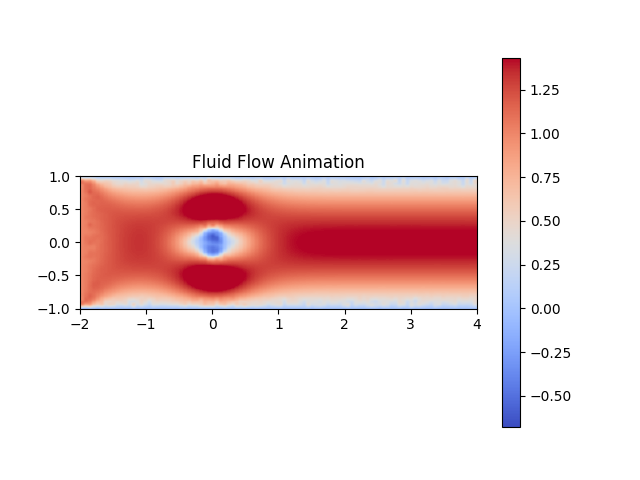
If we want to create an animtation of the data, we can write a separate function to achieve that goal:

def animate_flow(flow_data, interval=50):
    """
    Create an animation of the fluid flow.
    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    interval (int): Delay between frames in milliseconds
    Returns:
    matplotlib.animation.FuncAnimation: Animation object
    """
    # Your code here
    pass

def animate_flow(flow_data, interval=50):
    """
    Create an animation of the fluid flow.
    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    interval (int): Delay between frames in milliseconds
    Returns:
    matplotlib.animation.FuncAnimation: Animation object
    """
    fig, ax = plt.subplots()
    # Plot the initial frame
    im = ax.imshow(flow_data[0], cmap='coolwarm', animated=True, extent=[-2, 4, -1, 1])
    def update(frame):
        im.set_array(flow_data[frame])
        return [im]
    
    anim = FuncAnimation(fig, update, frames=flow_data.shape[0],
    interval=interval, blit=True)
    plt.colorbar(im)
    plt.title("Fluid Flow Animation")
    return anim

You can use the following code snippet to check the function’s output:

data = load_fluid_flow_data('cylinder_flow_data.npy')
anim = animate_flow(data)
plt.show()

Task 1.2: Reshape the Data for DMD

DMD requires the data to be in a specific format. We need to reshape our 3D flow field data (time, x, y) into a 2D matrix where each column represents a flattened snapshot of the flow field at a particular time.

def reshape_for_dmd(flow_data):
    """
    Reshape 3D flow data into a 2D matrix suitable for DMD.

    Parameters:
    flow_data (np.array): 3D array of shape (n_timesteps, n_x, n_y)

    Returns:
    np.array: 2D array of shape (n_x * n_y, n_timesteps)
    """
    # Your code here
    pass

def reshape_for_dmd(flow_data):
    """
    Reshape 3D flow data into a 2D matrix suitable for DMD.

    Parameters:
    flow_data (np.array): 3D array of shape (n_timesteps, n_x, n_y)

    Returns:
    np.array: 2D array of shape (n_x * n_y, n_timesteps)
    """
    n_timesteps, n_x, n_y = flow_data.shape
    return flow_data.reshape(n_timesteps, -1).T

Step 2: Implementing the DMD Algorithm

In this step, we’ll implement the core DMD algorithm. We’ll break it down into smaller functions to make it easier to understand and implement.

Task 2.1: Compute the DMD Matrices

Lets start with creating the matrices X1 and X2 needed for DMD analysis, and then compute the SVD of X1.

def compute_dmd_matrices(X):
    """
    Compute the matrices needed for DMD analysis.
    
    Parameters:
    X (np.array): 2D data matrix of shape (n_features, n_samples)
    
    Returns:
    tuple: (X1, X2) where X1 is X[:, :-1] and X2 is X[:, 1:]
    """
    # Your code here
    pass

def compute_svd(X):
    """
    Compute the Singular Value Decomposition (SVD) of a matrix.
    
    Parameters:
    X (np.array): 2D matrix
    
    Returns:
    tuple: (U, S, Vt) - The SVD components
    """
    # Use numpy's SVD function    
    # The SVD decomposition gives X = U * S * Vt, where:
    # U: Left singular vectors (columns are orthonormal)
    # S: Singular values (diagonal matrix, but returned as 1D array)
    # Vt: Right singular vectors (rows are orthonormal)
    
    # Note: full_matrices=False returns the compact SVD, which is more efficient for DMD
    
    # Your code here

    pass

def compute_dmd_matrices(X):
    """
    Compute the matrices needed for DMD analysis.
    
    Parameters:
    X (np.array): 2D data matrix of shape (n_features, n_samples)
    
    Returns:
    tuple: (X1, X2) where X1 is X[:, :-1] and X2 is X[:, 1:]
    """
    X1 = X[:, :-1]
    X2 = X[:, 1:]
    return X1, X2

def compute_svd(X):
    """
    Compute the Singular Value Decomposition (SVD) of a matrix.
    
    Parameters:
    X (np.array): 2D matrix
    
    Returns:
    tuple: (U, S, Vt) - The SVD components
    """
    # Use numpy's SVD function    
    # The SVD decomposition gives X = U * S * Vt, where:
    # U: Left singular vectors (columns are orthonormal)
    # S: Singular values (diagonal matrix, but returned as 1D array)
    # Vt: Right singular vectors (rows are orthonormal)
    
    # Note: full_matrices=False returns the compact SVD, which is more efficient for DMD
    
    U, S, Vt = np.linalg.svd(X, full_matrices=False)
    return U, S, Vt

You can use the following lines to check the functions:

import numpy as np
# Testing compute_dmd_matrices
X_test = np.random.rand(10, 5)
X1, X2 = compute_dmd_matrices(X_test)
assert X1.shape == (10, 4), "X1 should have one less column than X"
assert X2.shape == (10, 4), "X2 should have one less column than X"
assert np.array_equal(X1, X_test[:, :-1]), "X1 should be all but the last column of X"
assert np.array_equal(X2, X_test[:, 1:]), "X2 should be all but the first column of X"

# Testing compute_svd
X_svd_test = np.random.rand(10, 5)
U, S, Vt = compute_svd(X_svd_test)
assert U.shape == (10, 5), "U should have the same number of rows as X and min(X.shape) columns"
assert S.shape == (5,), "S should have length min(X.shape)"
assert Vt.shape == (5, 5), "Vt should be square with size min(X.shape)"
assert np.allclose(np.dot(U * S, Vt), X_svd_test), "SVD decomposition should satisfy X = U * S * Vt"
assert np.allclose(np.dot(U.T, U), np.eye(5)), "U should be orthonormal"
assert np.allclose(np.dot(Vt, Vt.T), np.eye(5)), "Vt should be orthonormal"

print("All tests passed successfully!")

Task 2.2: Compute DMD Modes and Eigenvalues

Now, we’ll use the results of the SVD to compute the DMD modes and eigenvalues. These represent the fundamental patterns and their temporal evolution in our fluid flow system.

The theory behind computing DMD modes and eigenvalues is as follows:

1. Given the SVD of X_1 (U, S, Vt) and X_2, we can approximate the linear operator A that maps X_1 to X_2:

   A ≈ X₂ * V * S^(-1) * U^T

2. We then compute the eigendecomposition of A:

   AW = WΛ

   where W are the eigenvectors and Λ are the eigenvalues.

3. The DMD modes Φ are then given by:

   Φ = X₂ * V * S^(-1) * W

4. The DMD eigenvalues are simply the eigenvalues Λ of A.

These DMD modes and eigenvalues capture the dominant spatial and temporal patterns in the data, respectively. The modes represent spatial structures, while the eigenvalues determine how these structures evolve over time.

def compute_dmd_modes_and_eigenvalues(U, S, Vt, X2):
    """
    Compute the DMD modes and eigenvalues.

    Parameters:
    U, S, Vt (np.array): SVD components of X1
    X2 (np.array): Second snapshot matrix

    Returns:
    tuple: (modes, eigenvalues)
    """
    # Your code here
    pass

def compute_dmd_modes_and_eigenvalues(U, S, Vt, X2):
    """
    Compute the DMD modes and eigenvalues.

    Parameters:
    U, S, Vt (np.array): SVD components of X1
    X2 (np.array): Second snapshot matrix

    Returns:
    tuple: (modes, eigenvalues)
    """
    # Compute the pseudoinverse of S
    S_inv = np.linalg.pinv(np.diag(S))
    
    # Compute the reduced DMD matrix
    A_tilde = U.T @ X2 @ Vt.T @ S_inv
    
    # Compute eigenvalues and eigenvectors of A_tilde
    eigenvalues, W = np.linalg.eig(A_tilde)
    
    # Compute the DMD modes
    modes = X2 @ Vt.T @ S_inv @ W
    
    return modes, eigenvalues

Step 3: Applying DMD to Fluid Flow Data

Now that we have implemented the core DMD algorithm, let’s apply it to our fluid flow data.

Task 3.1: Perform DMD on Fluid Flow Data

We write a function that combines all the previous steps to perform DMD on the fluid flow data. This function will give us the modes and eigenvalues that characterize our fluid flow system.

To develop this function, we need to understand the theory behind the DMD process:

1. Data Preparation:
   • Reshape the 3D flow_data array into a 2D matrix X, where each column represents a flattened snapshot.
   • Split X into X1 (all columns except the last) and X2 (all columns except the first).
2. Singular Value Decomposition (SVD):
   • Perform SVD on X1: X1 = U * S * Vt
   • Truncate the SVD to the first r modes for dimensionality reduction.

3. Compute the DMD operator:

   • Ã = U_r^T * X₂ * V_r * S_r^(-1)

   where U_r, V_r, and S_r are the truncated versions of U, V, and S.

4. Eigendecomposition of Ã:

   • Solve the eigenvalue problem: Ã * W = W * Λ where W are the eigenvectors and Λ are the eigenvalues.
5. Compute DMD modes:
   • Φ = X₂ * V_r * S_r^(-1) * W
6. Compute DMD dynamics:
   • Calculate the continuous-time eigenvalues: ω = log(Λ) / Δt, where Δt is the time step between snapshots (assumed to be 1/100 in this case).
   • Create a time vector t spanning the number of snapshots.
   • Compute the time dynamics: exp(ω * t), which can be efficiently calculated using np.exp(np.outer(ω, t)).
   • The resulting dynamics matrix will have dimensions (number of modes, number of timesteps).

With this theory in mind, we can now implement the function to perform DMD on the fluid flow data. We can implement reshape_for_dmd, compute_dmd_matrices, compute_svd, and compute_dmd_modes_and_eigenvalues functions within this function.

def perform_dmd(flow_data, r=10):
    """
    Perform DMD on the fluid flow data.

    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    r (int): Number of modes to retain

    Returns:
    tuple: (modes, eigenvalues, dynamics)
    """
    # Your code here
    pass

def perform_dmd(flow_data, r=10):
    """
    Perform DMD on the fluid flow data.

    Parameters:
    flow_data (np.array): 3D array of fluid flow data
    r (int): Number of modes to retain

    Returns:
    tuple: (modes, eigenvalues, dynamics)
    """
    # Reshape the data into a 2D matrix
    X = reshape_for_dmd(flow_data) 

    # Split the data into two snapshot matrices
    X1, X2 = compute_dmd_matrices(X)

    # Perform SVD on X1
    U, S, Vt = compute_svd(X1)

    # Truncate to r modes
    U_r = U[:, :r]
    S_r = S[:r]
    Vt_r = Vt[:r, :]

    # Compute DMD modes and eigenvalues
    modes, eigenvalues = compute_dmd_modes_and_eigenvalues(U_r, S_r, Vt_r, X2)

    # Compute mode dynamics
    n_timesteps = flow_data.shape[0]
    dt = 1/100  # Assuming 1/100 time step, adjust if necessary
    omega = np.log(eigenvalues) / dt
    t = np.arange(n_timesteps) * dt
    dynamics = np.exp(np.outer(omega, t))

    return modes, eigenvalues, dynamics

Step 4: Visualizing and Interpreting Results

In this final step, we’ll visualize the DMD results and interpret what they mean for our fluid flow system.

Task 4.1: Visualize DMD Modes

In this task, we’ll visualize the DMD modes and their corresponding frequencies. This will help us understand the spatial patterns and temporal behavior of the dominant fluid flow structures.

def plot_dmd_mode(mode, shape):
    """
    Plot a single DMD mode for fluid flow around a cylinder.
    
    Parameters:
    -----------
    mode (np.array): 1D array representing a DMD mode
        Complex-valued array that will be reshaped to 2D
        Only the real part will be visualized
    
    shape (tuple): Original shape of the flow field (n_x, n_y)
        Dimensions to reshape the mode into its 2D representation

    Expected Output:
    ---------------
    A single figure (10x8 inches) showing:
    - 2D visualization of the DMD mode
    - Grayscale colormap
    - Physical domain extent: x=[-2,4], y=[-1,1]
    - Cylinder shown as black circle at origin (radius=0.2)
    - Colorbar showing mode magnitude
    - Axis labels 'x' and 'y'
    - Title "DMD Mode"
    
    Visualization Details:
    ---------------------
    - Use imshow with aspect='equal'
    - Include cylinder as black circle at (0,0)
    - Show real part of mode only
    - Maintain physical dimensions using extent parameter
    - Add colorbar with label 'Mode Magnitude'

    Note:
    -----
    The visualization represents the spatial pattern of the mode
    in the physical domain around the cylinder, with darker and
    lighter regions showing the mode's structure.
    """
    pass

def plot_dmd_mode(mode, shape):
    """
    Plot a single DMD mode.
    
    Parameters:
    mode (np.array): 1D array representing a DMD mode
    shape (tuple): Original shape of the flow field (n_x, n_y)
    """
    import matplotlib.pyplot as plt
    import numpy as np

    # Reshape the mode to the original flow field shape
    mode_2d = mode.reshape(shape)

    # Create a figure and axis
    fig, ax = plt.subplots(figsize=(10, 8))

    # Plot the mode using imshow
    im = ax.imshow(np.real(mode_2d), cmap='gray', aspect='equal', 
                   extent=[-2, 4, -1, 1])

    # Add a colorbar
    plt.colorbar(im, ax=ax, label='Mode Magnitude')

    # Set title and labels
    ax.set_title('DMD Mode')
    ax.set_xlabel('x')
    ax.set_ylabel('y')

    # Add the cylinder
    circle = plt.Circle((0, 0), 0.2, fill=False, color='k')
    ax.add_artist(circle)

    plt.tight_layout()
    plt.show()

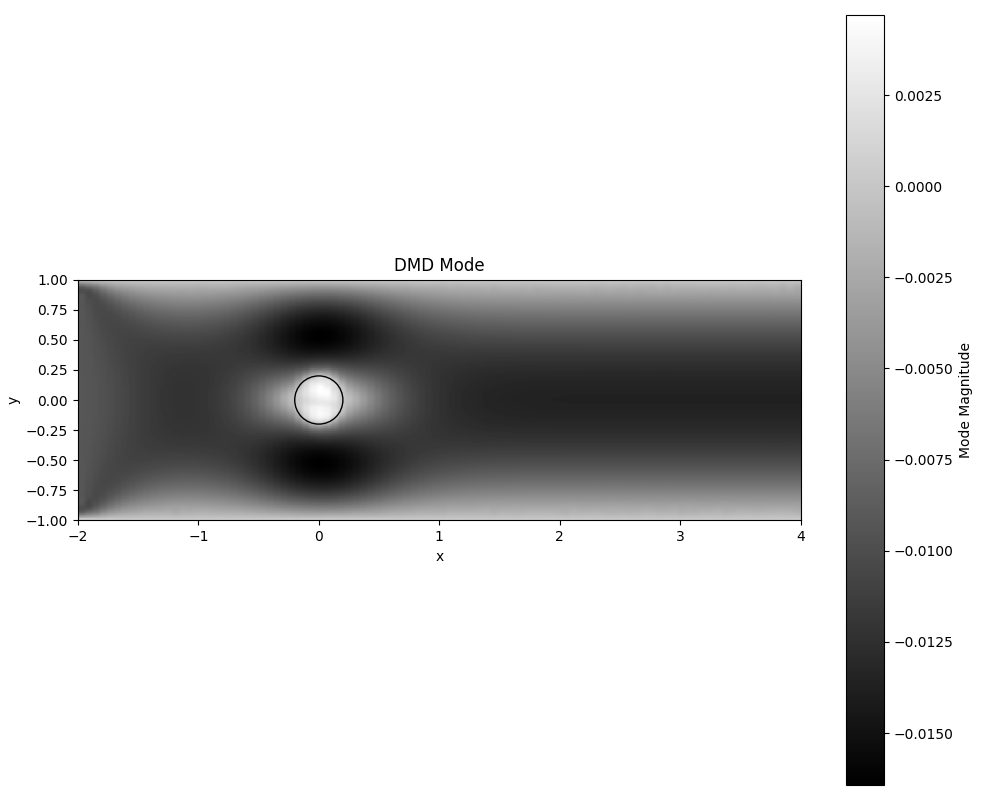
Understanding plot_dmd_mode

The plot_dmd_mode function helps us visualize individual DMD modes. Here’s what it does in simple terms:

1. What is a DMD mode?
   • A DMD mode is a spatial pattern in the fluid flow that evolves over time.
   • It represents a recurring structure or behavior in the flow.
2. What does the plot show?
   • The plot shows a 2D image of a single DMD mode.
   • The colors in the image represent the strength or importance of the mode at different locations.
   • Brighter areas show where the mode has a stronger effect on the flow.
   • Darker areas show where the mode has less influence.
3. How to interpret the plot:
   • Look for patterns: Are there areas of high intensity? Do you see any symmetries or recurring structures?
   • Compare with the original flow: How does this pattern relate to what you see in the overall flow?
   • Consider the location: Are there strong patterns near the cylinder or in the wake behind it?
4. Why is this useful?
   • It helps us identify important spatial structures in the flow.
   • We can see where the most significant flow behaviors are occurring.
   • By looking at multiple modes, we can build up a picture of the complex flow behavior.

def plot_mode_frequencies(eigenvalues, dt):
    """
    Plot the frequencies and growth rates of DMD modes.
    
    Parameters:
    -----------
    eigenvalues (np.array): DMD eigenvalues
        Complex-valued array containing temporal information
        Used to compute frequencies and growth rates
    
    dt (float): Time step between snapshots
        Time interval between data frames
        Used to convert eigenvalues to physical frequencies

    Expected Output:
    ---------------
    A single figure (10x5 inches) showing:
    - Scatter plot of mode frequencies vs growth rates
    - X-axis: Frequencies (computed as imag(log(λ))/(2π*dt))
    - Y-axis: Growth rates (computed as real(log(λ))/dt)
    - Red dashed line at y=0 separating growing/decaying modes
    - Grid lines for better readability
    
    Visualization Details:
    ---------------------
    - X-axis label: "Frequency"
    - Y-axis label: "Growth Rate"
    - Title: "DMD Mode Frequencies and Growth Rates"
    - Points above y=0: Growing modes
    - Points below y=0: Decaying modes

    Note:
    -----
    The plot helps identify:
    - Dominant frequencies in the flow
    - Stability of different modes (growing vs decaying)
    - Patterns in mode behavior
    """
    pass

def plot_mode_frequencies(eigenvalues, dt):
    """
    Plot the frequencies of the DMD modes.
    
    Parameters:
    eigenvalues (np.array): DMD eigenvalues
    dt (float): Time step between snapshots
    """
    frequencies = np.log(eigenvalues).imag / (2 * np.pi * dt)
    growth_rates = np.log(eigenvalues).real / dt
    
    plt.figure(figsize=(10, 5))
    plt.scatter(frequencies, growth_rates)
    plt.xlabel('Frequency')
    plt.ylabel('Growth Rate')
    plt.title('DMD Mode Frequencies and Growth Rates')
    plt.axhline(y=0, color='r', linestyle='--')
    plt.grid(True)
    plt.show()

Understanding plot_mode_frequencies

The plot_mode_frequencies function helps us visualize two important aspects of each DMD mode: its frequency and its growth rate.

1. Frequency:
   • Imagine a mode as a pattern in the fluid flow that repeats over time.
   • The frequency tells us how quickly this pattern repeats.
   • A higher frequency means the pattern repeats more often in a given time.
   • For example, a high-frequency mode might represent rapid, small-scale fluctuations in the flow.
2. Growth Rate:
   • The growth rate tells us whether the pattern is getting stronger or weaker over time.
   • A positive growth rate means the pattern is amplifying (getting stronger).
   • A negative growth rate means the pattern is decaying (getting weaker).
   • A growth rate near zero means the pattern stays about the same strength over time.
3. What does the plot show?
   • Each point on the plot represents one DMD mode.
   • The horizontal axis (x-axis) shows the frequency of each mode.
   • The vertical axis (y-axis) shows the growth rate of each mode.
   • The red dashed line at y=0 separates growing modes (above the line) from decaying modes (below the line).
4. How to interpret the plot:
   • Points on the right side represent high-frequency modes (fast-repeating patterns).
   • Points on the left side represent low-frequency modes (slow-repeating patterns).
   • Points above the red line are growing modes (getting stronger over time).
   • Points below the red line are decaying modes (getting weaker over time).
   • Points near the red line are relatively stable modes (neither growing nor decaying much).
5. Why is this useful?
   • It helps us identify which patterns (modes) are most important in the fluid flow.
   • We can see if there are any dominant frequencies in the flow.
   • We can tell if the flow has any unstable patterns that might grow over time.
   • It can help us understand the overall behavior of the fluid system.

In the context of fluid flow around a cylinder, you might see:

• Low-frequency modes representing the overall flow pattern around the cylinder.
• Higher-frequency modes that might correspond to vortex shedding behind the cylinder.
• Possibly some growing modes if the flow becomes unstable under certain conditions.

Both plot_dmd_mode and plot_mode_frequencies provide a comprehensive understanding of the key patterns in your fluid flow simulation, how they’re distributed in space, and how they behave over time.

# Testing the functions using the first 2 modes
flow_data = load_fluid_flow_data('cylinder_flow_data.npy')
modes, eigenvalues, dynamics = perform_dmd(flow_data, r=2)
plot_dmd_mode(modes[:,0], shape=(100,100))
dt = 0.01  # Assuming time step of 0.01
plot_mode_frequencies(eigenvalues, dt)

Task 4.2: Reconstruct and Compare Flow Fields

The theory behind reconstructing the flow field using DMD is as follows:

1. DMD Reconstruction: The DMD approximation of the flow field at time t is given by: x(t) ≈ Φ * b(t) where:
   • Φ are the DMD modes (spatial patterns)
   • b(t) are the mode amplitudes at time t (stored in dynamics matrix)
2. Matrix Implementation: For a specific timestep k:
   • Select the k-th column from dynamics matrix: b(k) = dynamics[:, k]
   • Multiply modes with dynamics: x(k) = modes @ b(k)
   • Take real part for physical solution
   • Reshape to original flow field dimensions

def reconstruct_flow_field(modes, dynamics, timestep):
    """
    Reconstruct the flow field at a given timestep using DMD.
    
    Parameters:
    -----------
    modes (np.array): DMD modes, shape (n_features, n_modes)
        Spatial patterns extracted by DMD
        Each column represents one spatial mode
    
    dynamics (np.array): DMD mode dynamics, shape (n_modes, n_timesteps)
        Temporal evolution of each mode
        Each row shows how one mode evolves over time
    
    timestep (int): Timestep to reconstruct
        Index of the time point to reconstruct
        Must be less than n_timesteps
    
    Returns:
    --------
    np.array: Reconstructed flow field, shape (n_x, n_x)
        2D array representing the reconstructed flow field
        Dimensions are square (n_x = sqrt(n_features))
        Contains real-valued flow field data

    Expected Steps:
    --------------
    1. Combine modes and dynamics at specified timestep
    2. Reshape result to square 2D array

    Note:
    -----
    - Input data should be properly normalized
    - Result will be real-valued (use np.real())
    - Assumes square flow field domain
    """
    # Your code here
    pass

def compare_original_and_reconstructed(original, reconstructed):
    """
    Compare the original and reconstructed flow fields visually and quantitatively.
    
    Parameters:
    -----------
    original (np.array): Original flow field, shape (n_x, n_x)
        2D array containing the original flow field data
        Used as ground truth for comparison
    
    reconstructed (np.array): Reconstructed flow field, shape (n_x, n_x)
        2D array containing the DMD-reconstructed flow field
        Should have same dimensions as original

    Expected Output:
    ---------------
    A single figure (12x5 inches) with:
    1. Left subplot:
       - Original flow field visualization
       - Title: "Original Flow Field"
       - Colormap: 'coolwarm'
       - Physical domain: x=[-2,4], y=[-1,1]
       - Colorbar showing flow values
    
    2. Right subplot:
       - Reconstructed flow field visualization
       - Title: "Reconstructed Flow Field"
       - Same colormap and domain as original
       - Colorbar showing flow values
    
    3. Overall figure:
       - Suptitle showing relative error
       - Equal aspect ratio for both plots
       - Tight layout

    Printed Metrics:
    ---------------
    - Mean Squared Error (MSE)
    - Mean Absolute Error (MAE)
    - Relative Error (norm of difference / norm of original)

    Note:
    -----
    - Both visualizations use same scale for fair comparison
    - Error metrics help quantify reconstruction quality
    - Lower error values indicate better reconstruction
    """
    # Your code here
    pass

def reconstruct_flow_field(modes, dynamics, timestep):
    """
    Reconstruct the flow field at a given timestep using DMD.
    
    Parameters:
    modes (np.array): DMD modes
    dynamics (np.array): DMD mode dynamics
    timestep (int): Timestep to reconstruct
    
    Returns:
    np.array: Reconstructed flow field
    """
    # Reconstruct the flow field by combining modes and dynamics
    reconstructed = np.real(np.dot(modes, dynamics[:, timestep]))
    
    # Reshape the reconstructed field to match the original dimensions
    original_shape = int(np.sqrt(reconstructed.shape[0]))
    reconstructed = reconstructed.reshape((original_shape, original_shape))
    
    return reconstructed

def compare_original_and_reconstructed(original, reconstructed):
    """
    Compare the original and reconstructed flow fields.
    
    Parameters:
    original (np.array): Original flow field
    reconstructed (np.array): Reconstructed flow field
    """
    # Create a figure with two subplots side by side
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

    # Plot original flow field
    im1 = ax1.imshow(original, cmap='coolwarm', aspect='equal', extent=[-2, 4, -1, 1])
    ax1.set_title('Original Flow Field')
    plt.colorbar(im1, ax=ax1)

    # Plot reconstructed flow field
    im2 = ax2.imshow(reconstructed, cmap='coolwarm', aspect='equal', extent=[-2, 4, -1, 1])
    ax2.set_title('Reconstructed Flow Field')
    plt.colorbar(im2, ax=ax2)

    # Compute and display the relative error
    relative_error = np.linalg.norm(original - reconstructed) / np.linalg.norm(original)
    plt.suptitle(f'Comparison (Relative Error: {relative_error:.4f})')

    plt.tight_layout()
    plt.show()

    # Print additional error metrics
    mse = np.mean((original - reconstructed)**2)
    mae = np.mean(np.abs(original - reconstructed))
    print(f'Mean Squared Error: {mse:.6f}')
    print(f'Mean Absolute Error: {mae:.6f}')

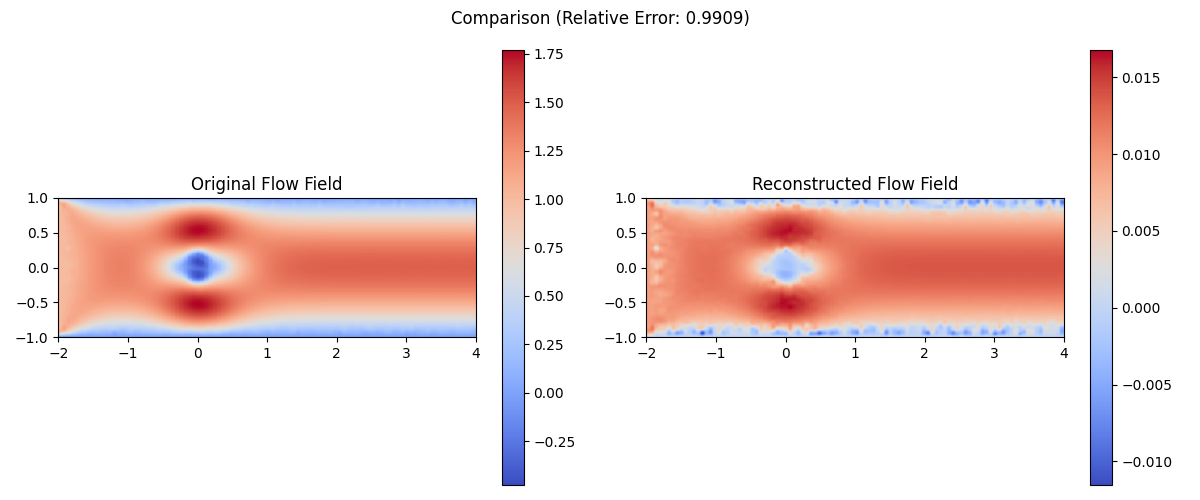
The following code sample can be used to test the functions:

# Loading the original data
original_data = load_fluid_flow_data('cylinder_flow_data.npy')
# Performing DMD 
modes, eigenvalues, dynamics = perform_dmd(original_data, r=10)  # r is the number of modes to retain

timestep = 50  # for example

# Reconstructing the flow field
reconstructed_field = reconstruct_flow_field(modes, dynamics, timestep)
# Comparing original and reconstructed fields
compare_original_and_reconstructed(original_data[timestep], reconstructed_field)

Interpreting the Outputs:

1. Reconstructed Flow Field:
   • The output of reconstruct_flow_field is a 2D array representing the reconstructed flow field at the specified timestep.
   • This field should resemble the original flow field, capturing the main features of the flow around the cylinder.
   • The accuracy of the reconstruction depends on the number of modes used in the DMD analysis.
2. Comparison Visualization:
   • The compare_original_and_reconstructed function should produce a side-by-side plot of the original and reconstructed flow fields.
   • Look for similarities in the overall structure of the flow, particularly around the cylinder and in the wake region.
   • Pay attention to the color scales: they should be similar for both plots if the reconstruction is accurate.
3. Number of Modes:
   • Try reconstructing the flow field with different numbers of DMD modes.
   • Generally, using more modes will improve the accuracy of the reconstruction but may also introduce noise or overfitting.
   • Find a balance where the reconstruction captures the important flow features without including too much detail that might be noise.

By comparing the reconstructed flow field with the original data, you can assess how well the DMD analysis has captured the essential dynamics of the system. This comparison helps validate the DMD results and provides insight into which flow features are most significant in the overall dynamics.

Conclusion

We’ve implemented the Dynamic Mode Decomposition algorithm from scratch and applied it to analyze 2D fluid flow around a cylinder. You’ve learned how to:

1. Prepare and preprocess fluid flow data for DMD analysis
2. Implement the core DMD algorithm, including SVD
3. Apply DMD to extract dominant modes and dynamics from fluid flow data
4. Visualize and interpret the results of DMD analysis

I hope this post has given you hands-on experience with a powerful data-driven method for analyzing complex fluid systems. The skills you’ve developed can be applied to a wide range of problems in fluid dynamics and other fields of engineering.